In dieser Serie beschäftige ich mich mit dem Hype-Thema 'Quantencomputer' (QC). Diese Disziplin der Informationstechnik ist mit vielen Hoffnungen und Ängsten aufgeladen. Werden wir bisher ungelöste Probleme in der Wettervorhersage lösen können, oder wird unsere Verschlüsselung gebrochen?
John von Neumann
Viele sehen Quantencomputer (QC) als weiteren Evolutionsschritt der klassischen Computer-Technologie. Diese Annahme ist falsch. QC ist ein ganz anderes Gebiet, das weder physikalisch, logisch, noch bei der praktischen Umsetzung mit bekannten Computern zu tun hat. Deshalb werden QC die bisherigen Computer eher nicht ersetzten, sondern ergänzen.
Bevor ich im nächsten Teil dieser Serie auf die logischen Grundlagen von QC eingehe, möchte ich in diesem Artikel auf die Basis herkömmlicher Computer zurückblicken. Zum einen ist dies wichtig, um den Unterschied zu QC klar zu erkennen, zum anderen sind diese Grundlagen vielen der Leserinnen vielleicht nicht mehr bewusst. Wie dem auch sei, ein Rückblick lohnt sich.
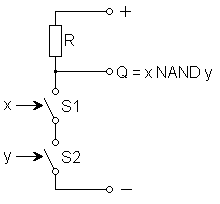
Wenn ich euch nach dem einfachsten Bild eines Computers fragen würde, was käme euch in den Sinn? Vielleicht eine Zuse-Z3, oder ein Commodore C64, oder doch lieber ein alter Assembler-Code. Mir kommt bei dieser Frage die Von-Neumann-Architektur aus dem Jahre 1945 in den Sinn. Dieses Konzept ist die Grundlage aller heute bekannten Computer. Um es in einem ganz einfachen Bild darzustellen, zeige ich euch dieses NAND-Gatter:
Was so einfach aussieht, ist die prinzipielle Grundlage aller klassischen Computer. Mit einem NAND-Gatter lässt sich mit ein paar Transistoren und Widerständen die gesamte Boolesche Algebra abbilden. Im Bild seht ihr einen Plus- und Minus-Pol, zwei Schalter (S1, S2) und einen Ausgang (Q). In einer aktuellen CPU von Intel oder AMD finden sich ca. 10 Milliarden solcher NAND-Gatter. Das Schöne an einem NICHT-UND-Gatter ist die Tatsache, dass sich damit (durch Kombinationen) alle Rechenoperationen abbilden lassen. Hier ein kleines Beispiel:
Schalter X ist aus (0) und Schalter Y (0) ist auch aus: Am Ausgang Q liegt nun eine positive Spannung an, also eine 1. Falls S1 oder (exklusiv) S2 geschlossen ist, liegt an Q immer noch 1 an, weil die Verbindung zwischen Plus und Minus noch nicht geschlossen ist. Erst wenn beide Schalter geschlossen sind, ist der Schaltkreis geschlossen und an Q liegt 0 an. Die Boolesche Tabelle für das NAND-Gatter sieht so aus:
| Eingang 1 | Eingang 2 | Ausgang (negiert) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Mit vier kombinierten NAND-Gattern lässt sich ein XOR-Gatter aufbauen, womit eine normale Addition von Zahlen möglich ist. In der Booleschen Tabelle für das XOR-Gatter, erkennt man sofort die Fähigkeit Zahlen zu addieren:
| Eingang 1 | Operation |
Eingang 2 | Operation |
Ausgang (= 2 Bit) |
| 0 | + | 0 | = | 0 = 00 |
| 0 | + | 1 | = | 1 = 01 |
| 1 | + | 0 | = | 1 = 01 |
| 1 | + | 1 | = | 0 (Übertrag 1) =10 |
Fazit: aus NAND-Gattern lassen sich alle anderen Booleschen Operation konstruieren, und damit alle denkbaren mathematischen Operationen. Egal, ob ihr eine AMD Ryzen CPU, eine Intel Rocket Lake CPU oder eine Nvidia Ampere GPU in eurem Rechner habt, es funktioniert alles mit NAND-Gattern.
Was hat das jetzt mit Quantencomputern zu tun? Nichts! Und genau darum geht es in diesem Artikel. Die Von-Neumann-Architektur basiert im Grunde genommen nur auf den physikalischen Zuständen von An oder Aus, Null oder Eins und den Booleschen Operationen. Die Logik von Quantencomputern ist eine ganz andere; an Stelle von Nullen und Einsen, treten hier Basiszustände, Wahrscheinlichkeiten und Superpositionen. Die Rolle der Booleschen Algebra nimmt bei QC die lineare Algebra (Matrizen) und die Wahrscheinlichkeitsrechnung ein. Der wichtigste Unterschied ist jedoch, dass wir bisher deterministisch (vorhersagbar) unterwegs waren und bei QC das neblige Feld der Probabilistik (Wahrscheinlichkeit) betreten werden - Gewissheit wird durch Hoffnung ersetzt!
Im zweiten Teil dieser Serie befasse ich mich mit der Logik der Quantencomputer. Spannend wird es dann im dritten Teil, in dem es um die Physik der QC gehen wird. Zum Schluss werde ich die praktischen Umsetzungen und Anwendungen unter die Lupe nehmen.
Den zweiten Teil der Artikelreihe könnt ihr hier lesen: https://gnulinux.ch/quantencomputer-teil-2-die-logik
Bildquellen:
https://commons.wikimedia.org/wiki/File:Funktionsprinzip_eines_NAND-Gatters.png
https://de.wikipedia.org/wiki/John_von_Neumann#/media/Datei:JohnvonNeumann-LosAlamos.gif