Quantencomputer - Teil 2 - Die Logik

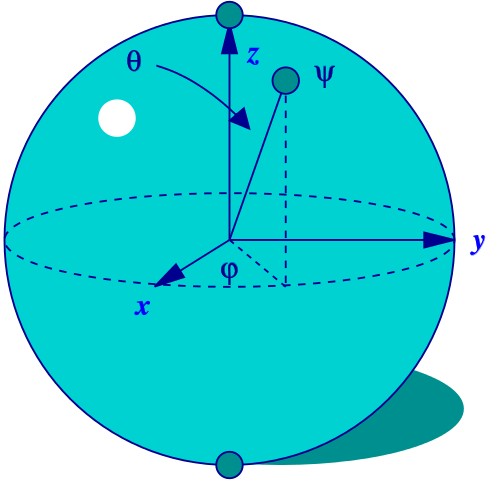
Im ersten Teil dieser Serie über Quantencomputer bin ich einen Schritt zurückgetreten, um die einfache Logik klassischer Computersysteme zu beschreiben. Ein paar Nullen und Einsen, das Binärsystem, die Boolesche Algebra und das NAND-Gatter als Grundbaustein. Während sich ein Bit anschaulich als elektrischer Schalter darstellen lässt (an oder aus), wird für Qubits (Quanten-Bits) häufig die Bloch-Kugel verwendet:

An den Polen befinden sich die Basiszustände (oben Null, unten Eins) des Qubits. Alle anderen Punkte verteilen sich über die Oberfläche dieser Kugel und werden Superposition genannt (im Bild der dritte graue Punkt rechts oben). Diese Position wird mit einem horizontalen und einem vertikalen Winkel angegeben und entspricht der Wahrscheinlichkeit, mit der der Zustand des Qubits gemessen werden kann. Wer bis hierher mitgekommen ist, sollte nicht verzagen; es wird schwieriger.

Ein Qubit verhält sich wie Schrödingers Katze, solange man nicht nachsieht (misst) befindet sich der Zustand des Qubits in einem Überlagerungszustand; die Katze ist gleichzeitig tot und lebendig. Erst beim Messen erhält man eine Information über den Zustand des Qubits und zerstört es damit sofort. Ein Qubit lässt sich nicht kopieren, weil sein Zustand beim Kopieren (Messen) zerstört würde.

Während die Leistung von klassischen Computern linear mit der Anzahl verwendeter Bits steigt, ist dieser Anstieg bei Qubits exponentiell; mit jedem weiteren Qubit verdoppelt sich die Leistung des Systems. Dies liegt an der Eigenschaft, dass sich zwei Qubits miteinander verschränken lassen. Dadurch entsteht ein neues System, bei welchem die Messung eines Qubits eine definierte Wahrscheinlichkeitsänderung bei der Messung des anderen Qubits bedeutet, und zwar unabhängig davon, wie weit die Qubits voneinander entfernt sind. Albert Einstein hat das als 'spukhafte Fernwirkung' bezeichnet und diese nicht verstanden. Der Begriff 'Ferne' führt dabei in die Irre, weil die verschränkten Qubits im Bereich der Quantenphysik keine 'Ferne' kennen; es ist ein System, unabhängig von der räumlichen Distanz. Anders ausgedrückt: wenn ich Qubit A messe, verhält sich Qubit B abhängig von A, egal wo sich A und B befinden.

In der Verschränkung liegt die Stärke der Qubits. Für Quantencomputer wichtig ist die Tatsache, dass durch die Verschränkung eines Satzes von n Qubits ein beliebiger Satz von Sequenzen n klassischer Bits gleichzeitig dargestellt werden kann. Beispielsweise kann mit vier Qubits ein Zustand hergestellt werden, der genau die Bitfolgen 0000, 0101, 1011 und 1110 enthält und keine anderen. Im Extremfall sind alle möglichen Bitfolgen darin enthalten, z.B. enthält ein entsprechend präpariertes 'Quantenbyte' alle Zahlen von 0 bis 255 gleichzeitig. Führt man nun mithilfe quantenmechanischer Operationen Berechnungen auf diesem Zustand aus, so werden diese Berechnungen effektiv auf allen diesen Bitfolgen gleichzeitig ausgeführt.

Ein Qubit lässt sich als Vektor (eindimensionale Matrix) darstellen. Der Zustand von mehreren Qubits wird durch das Tensorprodukt der Qubits dargestellt. Was bei herkömmlichen Computern die Logik-Gatter sind (AND, OR, NOT, usw.), sind bei Berechnungen mit Qubits, Gatter in Form von quadratischen Matrizen. Möchte man die Zustände von Qubits logisch miteinander kombinieren (rechnen), wendet man solche quantenmechanischen Gatter auf die Qubits an. Die bekanntesten Gatter sind das Hadamard-Gatter (bringt das Qubit in eine 50:50 Superposition), die verschiedenen Pauli-Gatter rotieren die Zustände des Qubits auf den x, y und z Achsen; damit entspricht z.B. ein Px-Gatter dem klassischen NOT-Gatter. Das Measurement-Gatter misst den Zustand eines Qubits und zerstört ihn danach. Das Ergebnis ist immer 0 oder 1.

Wann immer hier Qubits erwähnt wurden, sind logische Qubits gemeint. Um ein logische Qubit zu erhalten, werden zwischen 1'000 und 10'000 physische Qubits benötigt, um fehlerbereinigte Ergebnisse zu erhalten. Doch dazu mehr im dritten Teil dieser Serie.

Fazit

• Bei Qubits gelten nicht Einsen und Nullen, sondern Basiszustände (0, 1) und Wahrscheinlichkeiten (Superposition)
• Qubits lassen sich als Vektoren darstellen (Wahrscheinlichkeit der Position auf der Kugeloberfläche).
• Zum Programmieren universeller Quantengattercomputer wendet man definierte Logikgatter auf die Qubits an.
• Quantengatter definieren, wie zwischen den Zuständen von Qubits gewechselt wird.
• Quantengatter beschreibt man als Matrizen, also als lineare Transformation von Vektoren. Sie müssen immer quadratisch sein.
• Die Definition von eigenen Quantengattern ist sinnvoll um eigene Operation mit Qubits durchführen zu können.

Bildnachweis: https://en.m.wikipedia.org/wiki/File:Bloch-sphere-diagram.svg

Quelle: https://shop.heise.de/ix-special-2021-quantencomputer/Print