In den bisherigen Artikeln habe ich euch mit viel Theorie gequält, die sehr schwer zu verstehen ist. Für die letzte Folge dieser Serie, habe ich mir vorgenommen, ein möglichst einfaches Quanten-Programm vorzustellen. Das ist leichter als gesagt. Die Hauptquelle und Inspiration für diese Serie war das iX-Sonderheft zum Thema Quantencomputer. Auch darin gibt es praktische Beispiele, die allerdings so kompliziert sind, dass ich sie euch nicht zumuten möchte. Beim Quantencomputer-Bauer Rigetti habe ich etwas Einfacheres gefunden.
Das Beispielprogramm implementiert einen achtseitigen Würfel basierend auf der Quantenmechanik. Aufgrund der Einfachheit des Beispiels, treten die Quantenvorteile leider nicht deutlich in den Vordergrund; dafür ist es einigermassen verständlich. Bei Interesse könnt ihr nach dem Begriff 'simple quantum program' im Internet suchen und findet (schwierigen) Code ohne Ende.
Die klassische Umsetzung des Würfels (z.B. in Python) ist trivial:
import random
print(random.randint(1,8))So einfach dieser Code auch ist, wirklich zufällig sind die von Python generierten Zahlen nicht. Ein Quantenwürfel kann das besser, sofern er auf einem echten Quantencomputer ausgeführt wird.
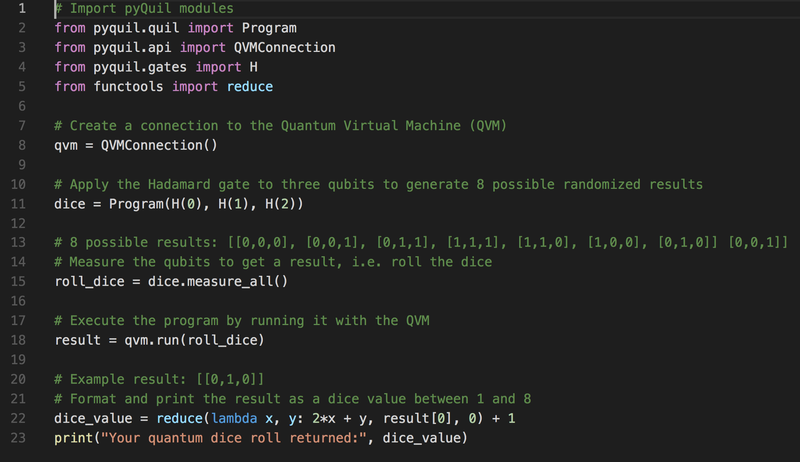
Anhand von Forest, dem Softwareentwicklungskit von Rigetti und seiner Python-basierten pyQuil-Bibliothek zeige ich ein Beispiel, wie dies in nur 10 Zeilen Code möglich ist. Konkret werden wir einen 8-seitigen Quantenwürfel bauen, der ein zufälliges Ergebnis erzeugt. Hier ist das Programm:
Ein Quantenwürfel aus 10 Zeilen Code
Einrichtung und Installation
Rigetti bietet mit dem Forest-SDK eine Entwicklungsumgebung für Quanten-Processing an. Um damit arbeiten zu können, muss man sich zuerst einen kostenlosen API-Schlüssel besorgen. Nach der Anmeldung erhält man den Key per E-Mail zugesandt. Eine weitere Voraussetzung ist Python v3.x.
Alsdann wird pyQuil benötigt. PyQuil ist eine Python-Bibliothek für die Quantenprogrammierung unter Verwendung von Quil, der bei Rigetti Computing entwickelten Quantenbefehlssprache. PyQuil bietet drei Hauptfunktionen:
- Einfaches Erzeugen von Quil-Programmen aus Quantengattern und klassischen Operationen
- Kompilieren und Simulieren von Quil-Programmen mit Hilfe des Quil-Compilers (quilc) und der Quantum Virtual Machine (QVM)
- Ausführen von Quil-Programmen auf echten Quantenprozessoren (QPUs) unter Verwendung von Quantum Cloud Services (QCS)
PyQuil installiert man entweder mit: conda install -c rigetti pyquil oder mit pip. Dann öffnet man einen Code-Editor (oder ein Jupyter-Notebook) und legt die Datei quantum_dice.py an:
Am Anfang der Datei importieren wir das Folgende:
from pyquil.quil import Program
from pyquil.api import QVMConnection
from pyquil.gates import H
from functools import reduceqvm = QVMConnection()Was haben wir hier importiert?
- Quantum-Programme werden in Forest unter Verwendung des Program-Objekts geschrieben, das die Hauptlogik der Anwendung aufnimmt.
- QVMConnection ermöglicht es, eine Verbindung zu einer virtuellen Quantenmaschine (QVM) herzustellen, einem leistungsstarken 26-Qubit-Simulator eines Quantencomputers.
- H ist das Hadamard-Gatter. Keine Sorge, für den Moment muss man nur wissen, dass es einen Quantenzustand anwendet, der uns hilft, das Würfeln zu randomisieren.
- reduce ist kein Bestandteil von pyQuil, sondern eine in Python häufig verwendete Funktion zur Durchführung von Schleifen und iterativen Berechnungen. Sie hilft uns insbesondere dabei, das Endergebnis unseres Würfelns in einen ganzzahligen Wert zwischen 1 und 8 zu formatieren.
Qubits, Überlagerung und Quantengatter
Bevor wir weitermachen, hier nochmal eine kurze Wiederholung der Konzepte der Quanteninformatik:
In klassischen Computern (z.B. unseren Laptops, Telefonen usw.) werden alle Interaktionen und Informationen, die wir erzeugen, schliesslich in eine Reihe von binären Bits umgewandelt: 0en oder 1en.
In der Quanteninformatik haben wir Quantenbits, oder Qubits. Das Besondere an Qubits ist, dass sie nicht binär sind, d.h. sie können sich in einem Zustand von 0, 1 oder einem speziellen Zwischenzustand befinden, der als Superposition bezeichnet wird. In der Superposition ist ein Qubit gleichzeitig 0 und 1. Wenn wir das Qubit messen, kollabiert es aus seinem Quantenzustand und liefert entweder eine 0 oder eine 1.
Betrachten wir folgende Analogie: Ein Ball ist zu Beginn entweder rot oder blau (sein Anfangszustand). Wir legen diesen Ball in eine geschlossene Schachtel, und während er sich in der Schachtel befindet, nutzt der Ball einige Quanteneigenschaften, um seine Farbe in Lila zu ändern - eine Zwischenkombination aus Rot und Blau (d. h. Superposition). Wenn wir die Schachtel öffnen, um den violetten Ball zu beobachten, ändert er plötzlich wieder seine Farbe und wir sehen nur noch entweder einen roten oder einen blauen Ball (aka Katze).
Wir verwenden Quantengatter, um den Zustand unserer Qubits zu ändern und sie zu kontrollieren, während sie sich in Überlagerung befinden. Es handelt sich dabei um Quantenoperationen, die den klassischen booleschen Logikgattern (z. B. NOT, AND, XOR usw.) entsprechen, aber aufgrund ihrer Quanteneigenschaft zusätzliche Funktionen aufweisen.
Zum Beispiel ändert das quantumX-Gatter den Zustand eines Qubits von 0 auf 1. Das Hadamard-Gatter, H-Gatter, versetzt ein Qubit in Superposition und erzeugt eine 50/50-Zufallswahrscheinlichkeit, entweder eine 0 oder eine 1 zu messen. Mit pyQuil können wir diese Gatter einfach in unser Programm importieren.
Erstellen des 8-seitigen Würfels mit Quantenbits
Um zu veranschaulichen, wie das funktioniert, kehren wir zu unserem Quantenwürfelprogramm zurück.
dice = Programm(H(0), H(1), H(2))Hier verwenden wir das H-Gatter oder Hadamard-Gatter, das wir zuvor importiert haben. Zuerst geben wir ein einzelnes Qubit ein: H(0). In pyQuil werden die Qubits beginnend mit 0, 1, 2, usw. indiziert. Wir wiederholen dies für zwei weitere Qubits: H(1), H(2). Jetzt haben wir drei Qubits - jedes in Überlagerung und jedes mit einer zufälligen Wahrscheinlichkeit, entweder 0 oder 1 zu ergeben, wenn sie gemessen werden. Damit haben wir insgesamt 8 mögliche Ergebnisse (2 * 2 * 2 = 2³), die jede Seite unseres Quantenwürfels darstellen werden:
[0, 0, 0] Alle drei Qubits befinden sich im Zustand 0
[0, 0, 1] Die ersten beiden Qubits sind im Zustand 0, das dritte im Zustand 1
[0, 1, 1] Das erste Qubit ist im Zustand 0, das zweite und dritte im Zustand 1
[1, 1, 1] ...
[1, 1, 0]
[1, 0, 1]
[1, 0, 0]
[0, 1, 0]
Ihr habt vielleicht bemerkt, dass jedes zusätzliche Qubit, das wir zu unserem Programm hinzufügen, die Anzahl der Seiten unseres Würfels verdoppelt. Ein viertes Qubit würde also einen 16-seitigen Würfel erzeugen; fünf Qubits würden einen 32-seitigen Würfel erzeugen, und so weiter. Dies veranschaulicht eines der grundlegenden Prinzipien, die Quantencomputer so leistungsfähig machen: Die Leistung von Quantencomputern skaliert exponentiell mit den Qubits (d.h. N Qubits = 2^N Bits). Wir brauchten nur drei Qubits, um 8 mögliche Ergebnisse zu erzeugen.
Würfeln
Nun, da wir 8 gleichermassen zufällige Ergebnisse haben, müssen wir ein einziges Ergebnis erzeugen, d. h. würfeln. Nennen wir diese Funktion roll_dice:
# Messen der Qubits, um ein Ergebnis zu erhalten
roll_dice = dice.measure_all()In einer Quantenumgebung führt eine Messung dazu, dass ein Qubit aus der Superposition kollabiert. Wenn wir also die Methode measure.all() aufrufen, kollabiert jedes unserer Qubits in einen zufälligen Zustand von entweder 0 oder 1. Effektiv erzeugt unsere Messung einen zufälligen "Würfelwurf". Um zu unserer roll_dice-Funktion zurückzukehren, führen wir sie aus, indem wir sie mit der QVM (Quantum Virtual Machine) ausführen:
result = qvm.run(roll_dice)Ein Beispiel für ein Ergebnis, das durch die Ausführung dieser Funktion erzeugt wird, ist [[0,1,0]]. Die innere Liste stellt den Endzustand unserer drei Qubits dar - eine der 8 oben aufgeführten Möglichkeiten (d.h. das Ergebnis unseres Würfelwurfs).
Zum Schluss formatieren wir das Ergebnis in einen gut lesbaren Würfelwert zwischen 1 und 8. Wir verwenden die Funktion reduce, die wir zuvor importiert haben, um unser Ergebnis von einer Liste von drei Qubit-Zuständen in eine einzelne Ganzzahl umzuwandeln:
dice_value = reduce(lambda x, y: 2*x + y, result[0], 0) + 1
print("Dein Quantenwürfelwurf ergab:", dice_value)Der Wechsel von der QVM zur QPU
Zusammenfassend lässt sich sagen, dass wir mit Rigettis virtueller Quantenmaschine erfolgreich einen achtseitigen Würfel auf einem Quantencomputer simuliert haben. Nun wollen wir sehen, wie wir dies auf dem eigentlichen Quantencomputer selbst tun können.
Die Quantenverarbeitungseinheiten (QPUs) oder Quantenchips von Rigetti werden in einem Labor in Fremont, Kalifornien, hergestellt, dann verdrahtet und in einen Kryostaten in Berkeley, Kalifornien, integriert, wo sie über die Cloud verfügbar gemacht werden. Derzeit ist der Agave 8-Qubit-Chip (8Q-Agave) in Betrieb und kann über die Forest-API angeschlossen werden. Ihr könnt den Zugriff auf die QPU hier beantragen. Der Zugang wird dann für ein bestimmtes Zeitfenster geplant. Sobald der Zugang erteilt wurde, könnt ihr eure Verbindung zum QVM mit wenigen Codezeilen durch eine Verbindung zum QPU ersetzen:
# Entferne dies
from pyquil.api import QVMConnection
...qvm = QVMConnection()
....result = qvm.run(roll_dice)
Und verbinde dich sich mit der QPU:
from pyquil.api import QPUConnection
...qpu = QPUConnection('8Q-Agave')
...result = qpu.run(roll_dice)Fazit
Diese Serie war harte Kost; nicht nur für euch, sondern auch für mich. Es ist besonders schwierig über Dinge zu schreiben, von denen man (fast) keine Ahnung hat. Die meisten Inputs stammen aus dem iX-Sonderheft 'Quantencomputer', welches ich zum Kauf empfehlen möchte, aber nur, wenn ihr euch wirklich für das Thema interessiert. Dort werden auf 160 Seiten und in 21 Beiträgen Quantencomputer von vorne bis hinten erklärt. Einfacher als in meiner Serie ist das Heft jedoch nicht; dafür sehr viel ausführlicher.
Meine Take-aways aus der Serie sind:
- Quantencomputer funktionieren vollkommen anders, als klassische Computer.
- Das angestammte Informatikwissen der letzten 30 Jahre hilft in diesem Bereich sehr wenig.
- Die Grundlagen sind schwer zu verstehen, was in der Natur der Sache liegt.
- Trotzdem liegt in Quantencomputern die Zukunft, weshalb es sich lohnt, sich damit zu beschäftigen und zu lernen.
Mein Ratschlag: Begebt euch in Superposition und schaut nach, was nach dem Öffnen des Kastens bei euch hängengeblieben ist.
Quellen: